2024-01-29发表2025-02-28更新leetcode1 小时读完 (大约10440个字)

leetcode-二叉树

二叉树

1、二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

1 2	输入：root = [1,null,2,3] 输出：[1,2,3]

示例 2：

1 2	输入：root = [] 输出：[]

示例 3：

1 2	输入：root = [1] 输出：[1]

示例 4：

1 2	输入：root = [1,2] 输出：[1,2]

示例 5：

1 2	输入：root = [1,null,2] 输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

// 递归算法
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        preOrder(root, result);
        return result;

    }
    public void preOrder(TreeNode root,List<Integer> result) {
        if (root == null) {
            return;
        }
        result.add(root.val);
        preOrder(root.left, result);
        preOrder(root.right, result);
    }
}

// 迭代算法
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            if(node.right != null) {
                stack.push(node.right);
            }
            if(node.left != null) {
                stack.push(node.left);
            }
        }
        return result;
    }

}

2、二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

1 2	输入：root = [1,null,2,3] 输出：[3,2,1]

示例 2：

1 2	输入：root = [] 输出：[]

示例 3：

1 2	输入：root = [1] 输出：[1]

提示：

树中节点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

方案一：递归的方法

1.确定递归函数的返回值，参数

2.确定递归函数的终止条件

3.确定单层递归的逻辑

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        postorderTraver(root,result);
        return result;
    }
    public void postorderTraver(TreeNode root, List<Integer> result) {
        if(root == null) return;
        postorderTraver(root.left,result);
        postorderTraver(root.right,result);
        result.add(root.val);
    }
}

迭代法：

class Solution { 
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            if(node.left != null) {
                stack.push(node.left);
            }
            if(node.right != null) {
                stack.push(node.right);
            }
        }
        // int firstIndex = 0;
        // int secondIndex = result.size() - 1; // 使用 size() 方法获取列表的大小
        // while (firstIndex < secondIndex) {
        //     Integer temp = result.get(firstIndex); // 使用 get(index) 方法访问列表中的元素
        //     result.set(firstIndex, result.get(secondIndex)); // 使用 set(index, value) 方法设置列表中的元素
        //     result.set(secondIndex, temp);
        //     firstIndex++;
        //     secondIndex--;
        // }
        Collections.reverse(result);
        return result;  
    }
}

3、二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

1 2	输入：root = [1,null,2,3] 输出：[1,3,2]

示例 2：

1 2	输入：root = [] 输出：[]

示例 3：

1 2	输入：root = [1] 输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorderTraver(root,result);
        return result;
    }
    public void inorderTraver(TreeNode root, List<Integer> result) {
        if (root == null) return;
        inorderTraver(root.left,result);
        result.add(root.val);
        inorderTraver(root.right,result);
    }
}

迭代法：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        } 
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        TreeNode cur = root;
        while (!stack.isEmpty())  {
            if (cur.left != null) {
                stack.push(cur.left);
                cur = cur.left;
            } else {
                TreeNode node = stack.pop();
                result.add(node.val);
                if(node.right != null) {
                    stack.push(node.right);
                    cur = node.right;
                }                
            }
        }
        return result;
    }
}

4、二叉树的统一迭代法

 // 非递归前序遍历，统一迭代法
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<Integer>();
        Stack<TreeNode> stack = new Stack<>();
        if (root == null) return result;
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode tmp = stack.peek();
            if (tmp != null){
                stack.pop();
                if(tmp.right != null){
                    stack.push(tmp.right);
                }
                if(tmp.left != null){
                    stack.push(tmp.left);
                }
                stack.push(tmp);
                stack.push(null);
            }else {
                stack.pop();
                TreeNode target = stack.pop();
                result.add(target.val);
            }
        }
        return result;
    }
}

// 非递归中序遍历，统一迭代法
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root == null) return result;
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode temp = stack.peek();
            if(temp != null){
                stack.pop();
                if(temp.right != null) {
                    stack.push(temp.right);
                }
                stack.push(temp);
                stack.push(null);
                if(temp.left !=null) {
                    stack.push(temp.left);
                }
            }else {
                stack.pop();
                TreeNode target = stack.pop();
                result.add(target.val); 
            }
        }
        return result;

    }
}

// 非递归后续遍历，统一迭代法 
class Solution { 
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root == null) return result;
        stack.push(root);
        while(!stack.isEmpty()) {
            TreeNode temp = stack.peek();
            if(temp != null) {
                stack.push(null);
                if(temp.right != null) {
                    stack.push(temp.right);
                }
                if(temp.left != null) {
                    stack.push(temp.left);
                }
            } else {
                stack.pop();
                TreeNode target = stack.pop();
                result.add(target.val);
            }
        }
        return result;
    }
}

5、二叉树的层序遍历

https://leetcode.cn/problems/binary-tree-level-order-traversal/

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

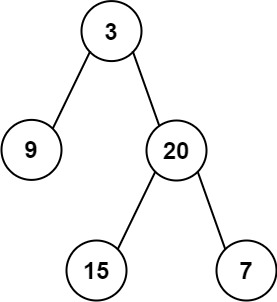
1 2	输入：root = [3,9,20,null,null,15,7] 输出：[[3],[9,20],[15,7]]

示例 2：

1 2	输入：root = [1] 输出：[[1]]

示例 3：

1 2	输入：root = [] 输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        if (root == null) return result;
        Queue<TreeNode> treeQue = new LinkedList<TreeNode>();
        treeQue.offer(root);
        while (!treeQue.isEmpty()){
            int size = treeQue.size();
            List <Integer> itemList = new ArrayList<Integer>();
            while(size > 0){
                TreeNode item = treeQue.poll();
                itemList.add(item.val);
                if(item.left != null){
                    treeQue.offer(item.left);
                }
                if(item.right != null){
                    treeQue.offer(item.right);
                }
                size--;
            }
            result.add(itemList);
        }
        return result;
    }
}

一口气打10题：

102.二叉树的层序遍历(opens new window)

107.二叉树的层次遍历II(opens new window)

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1：

1 2	输入：root = [3,9,20,null,null,15,7] 输出：[[15,7],[9,20],[3]]

示例 2：

1 2	输入：root = [1] 输出：[[1]]

示例 3：

1 2	输入：root = [] 输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> result = new LinkedList<List<Integer>>();
        if (root == null) {
            return result;
        }
        Queue <TreeNode> treeQue = new LinkedList<TreeNode>();
        treeQue.offer(root);
        while (!treeQue.isEmpty()) {
            int size = treeQue.size();
            List<Integer> itemList = new ArrayList<Integer>();
            while (size > 0) {
                TreeNode tmp = treeQue.poll();
                itemList.add(tmp.val);
                if (tmp.left != null) {
                    treeQue.offer(tmp.left);
                }
                if (tmp.right != null) {
                    treeQue.offer(tmp.right);
                }
                size--;
            }
            result.add(0,itemList);
        }
        return result;

    }
}

在 Java 的 LinkedList 类中，add(int index, E element) 方法用于在指定位置 index 插入元素 element。当我们使用 result.add(0, itemList);，这意味着我们每次都在 result 列表的开头位置插入一个新的列表 itemList。

下面是这个操作背后的一些底层细节：
LinkedList 是一个双向链表。每个元素（或称为节点）都包含三个部分：存储的数据、指向前一个元素的链接和指向下一个元素的链接。
在开头插入（index = 0）：当在链表的开始处插入一个新元素时，新元素成为新的头节点。新的头节点的“下一个”链接指向原来的头节点，如果原来的链表不是空的，则原来的头节点的“前一个”链接更新为指向新的头节点。此操作的时间复杂度为 O(1)，因为不需要遍历链表即可完成插入。

更新头尾指针：如果链表原来是空的，则新插入的节点既是头节点也是尾节点。如果链表不是空的，只需更新头节点指针（对于在开头插入的情况）

199.二叉树的右视图(opens new window)

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

1 2	输入: [1,2,3,null,5,null,4] 输出: [1,3,4]

示例 2:

1 2	输入: [1,null,3] 输出: [1,3]

示例 3:

1 2	输入: [] 输出: []

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

```



- [637.二叉树的层平均值(opens new window)](https://leetcode.cn/problems/average-of-levels-in-binary-tree/)
- [429.N叉树的层序遍历(opens new window)](https://leetcode.cn/problems/n-ary-tree-level-order-traversal/)
- [515.在每个树行中找最大值(opens new window)](https://leetcode.cn/problems/find-largest-value-in-each-tree-row/)
- [116.填充每个节点的下一个右侧节点指针(opens new window)](https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/)
- [117.填充每个节点的下一个右侧节点指针II(opens new window)](https://leetcode.cn/problems/populating-next-right-pointers-in-each-node-ii/)
- [104.二叉树的最大深度(opens new window)](https://leetcode.cn/problems/maximum-depth-of-binary-tree/)
- [111.二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/)

#### 6、翻转二叉树

给你一棵二叉树的根节点 `root` ，翻转这棵二叉树，并返回其根节点。

 

**示例 1：**

![img](https://assets.leetcode.com/uploads/2021/03/14/invert1-tree.jpg)

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]


**示例 2：**

![img](https://assets.leetcode.com/uploads/2021/03/14/invert2-tree.jpg)

输入：root = [2,1,3]
输出：[2,3,1]

1
2
3


**示例 3：**

输入：root = []
输出：[]


**提示：**

- 树中节点数目范围在 `[0, 100]` 内
- `-100 <= Node.val <= 100`

```java
//方案一，递归法（前序、后序都可以）
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        swapTree(root);
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
    public void swapTree(TreeNode root) {
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}

//迭代法 （深度优先遍历）统一迭代法
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null){
            return root;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()) {
            TreeNode temp = stack.peek();
            if (temp != null) {
                stack.pop();
                if (temp.right != null) {
                    stack.push(temp.right);
                }
                stack.push(temp);
                stack.push(null);
                if (temp.left != null) {
                    stack.push(temp.left);
                }
            } else {
                stack.pop();
                TreeNode target = stack.pop();
                swapTree(target);
            }
        }
        return root;
    }
    public void swapTree(TreeNode root) {
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}

//迭代法 （广度优先遍历即层序遍历）
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while(!deque.isEmpty()) {    
            for (int size = deque.size(); size > 0; size--) {
                TreeNode temp = deque.poll();
                swapTree(temp);
                if (temp.left != null) {
                    deque.offer(temp.left);
                }
                if (temp.right != null) {
                    deque.offer(temp.right);
                }
            }
        }
        return root;
    }
    public void swapTree(TreeNode root) {
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}

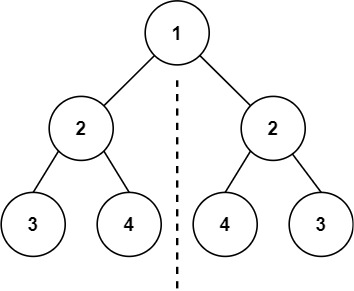
7、对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

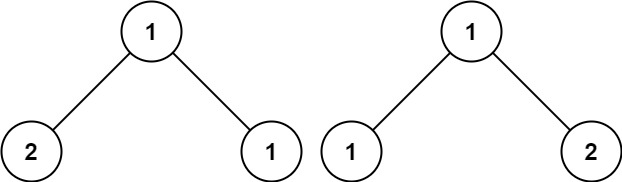
1 2	输入：root = [1,2,2,3,4,4,3] 输出：true

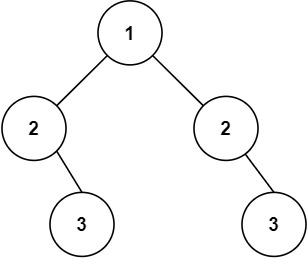
示例 2：

1 2	输入：root = [1,2,2,null,3,null,3] 输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

// 递归法
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return compare(root.left,root.right);
    }
    public boolean compare(TreeNode left, TreeNode right) {
        if (left == null && right != null) {
            return false;
        } 
        if (left != null && right == null) {
            return false;
        }  
        if (left == null && right == null) {
            return true;
        }
        if (left.val != right.val) {
            return false;
        } 
        boolean outside = compare(left.left,right.right);
        boolean inside = compare(left.right,right.left);
        return outside && inside;
    }
}

// 迭代法
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        Deque <TreeNode> deque = new LinkedList<>();
        deque.offer(root.left);
        deque.offer(root.right);
        while(!deque.isEmpty()) {
            TreeNode right = deque.poll();
            TreeNode left = deque.poll();
            if(right == null && left != null) {
                return false;
            }
            if(right != null && left == null) {
                return false;
            }
            if(right == null && left == null) {
                continue;
            }
            if(right.val != left.val) {
                return false;
            }
            deque.offer(left.left);
            deque.offer(right.right);
            deque.offer(left.right);
            deque.offer(right.left);
        }
        return true;
    }
}

两道相似的题：

100.相同的树(opens new window)

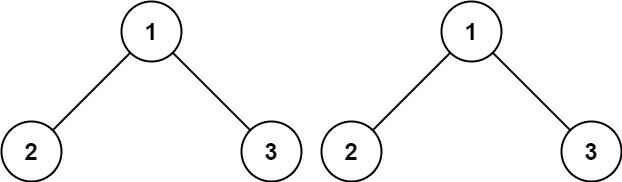
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

1 2	输入：p = [1,2,3], q = [1,2,3] 输出：true

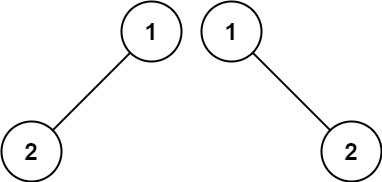
示例 2：

1 2	输入：p = [1,2], q = [1,null,2] 输出：false

示例 3：

1 2	输入：p = [1,2,1], q = [1,1,2] 输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-10^4 <= Node.val <= 10^4

//递归法
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q != null) {
            return false;
        }
        if (p != null && q == null) {
            return false;
        }
        if (p == null && q == null) {
            return true;
        }
        if (p.val != q.val) {
            return false;
        }
        boolean left = isSameTree(p.left,q.left);
        boolean right = isSameTree(p.right,q.right);
        return left && right;
    }
}

//递归法
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        Deque <TreeNode> deque = new LinkedList<>();
        deque.offer(p);
        deque.offer(q);
        while(!deque.isEmpty()) {
            TreeNode rightTree = deque.poll();
            TreeNode leftTree = deque.poll();
            if (rightTree == null && leftTree !=null) {
                return false;
            }
            if (rightTree != null && leftTree == null) {
                return false;
            }
            if (rightTree == null && leftTree == null) {
                continue;
            }
            if (rightTree.val != leftTree.val) {
                return false;
            }
            deque.offer(rightTree.left);
            deque.offer(leftTree.left);
            deque.offer(rightTree.right);
            deque.offer(leftTree.right);
        }
        return true;
    }

572.另一个树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

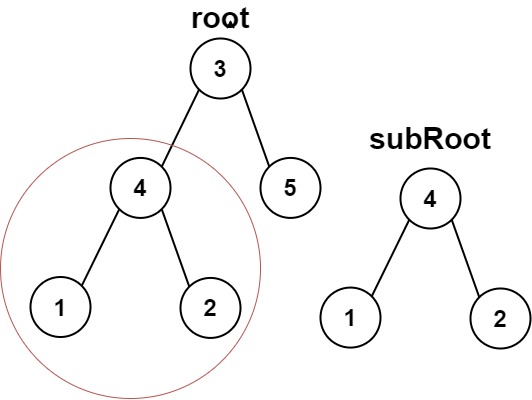
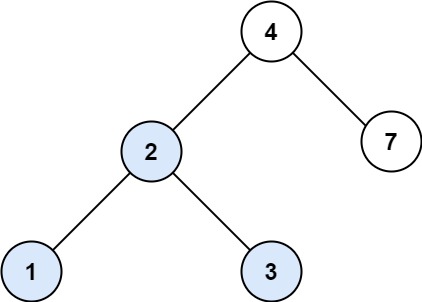
1 2	输入：root = [3,4,5,1,2], subRoot = [4,1,2] 输出：true

示例 2：

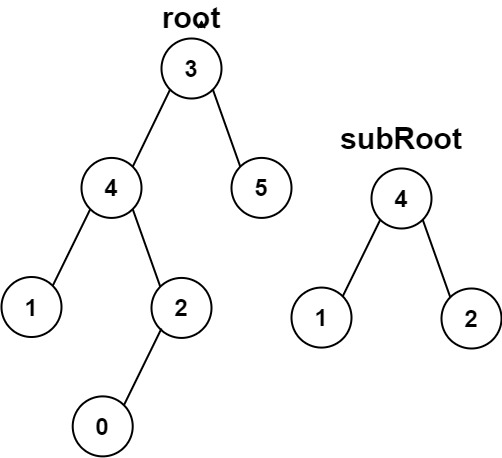
1 2	输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 输出：false

提示：

root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null) {
            return false;
        }
        if (isSametree(root,subRoot)) {
            return true;
        }
        return isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
    }

    public boolean isSametree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        if (p.val != q.val) {
            return false;
        }
        boolean left = isSametree(p.left,q.left);
        boolean right = isSametree(p.right,q.right);
        return left && right;
    }
}

1	//有一种树哈希的算法

1	//转化为字符串序列用kmp算法

8、二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

1 2	输入：root = [3,9,20,null,null,15,7] 输出：3

示例 2：

1 2	输入：root = [1,null,2] 输出：2

提示：

树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100

class Solution {
    public int maxDepth(TreeNode root) {
        int depth = 0;
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left)+1,maxDepth(root.right)+1);
    }
}

559.n叉树的最大深度(opens new window)

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

1 2	输入：root = [1,null,3,2,4,null,5,6] 输出：3

示例 2：

1 2	输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出：5

提示：

树的深度不会超过 1000 。
树的节点数目位于 [0, 104] 之间。


class Solution {
    public int maxDepth(Node root) {
        int depth = 0;
        if (root == null) {
            return 0;
        }
        for (int i = 0;i<root.children.size();i++) {
            depth = Math.max(depth,maxDepth(root.children.get(i)));
        }
        return depth+1;    
    }
}

9、二叉树的最小深度

力扣题目链接

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

1 2	输入：root = [3,9,20,null,null,15,7] 输出：2

示例 2：

1 2	输入：root = [2,null,3,null,4,null,5,null,6] 输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

// 层序遍历
class Solution {
    public int minDepth(TreeNode root) {
        int depth = 0 ;
        if (root == null) {
            return depth;
        }
        Deque <TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            depth++;
            for (int i = deque.size(); i > 0 ; i--) {
                TreeNode tmp = deque.poll();
                if (tmp.left != null) {
                    deque.offer(tmp.left);
                }
                if (tmp.right != null) {
                    deque.offer(tmp.right);
                }
                if(tmp.left == null && tmp.right == null) {
                    return depth;
                }
             }
        }
        return depth;
    }
}

class Solution {
    public int minDepth(TreeNode root) {
        int depth = 0 ;
        if (root == null) {
            return 0;
        }
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        if (root.left == null) {
            depth = right+1;
        }
        if (root.right == null) {
            depth = left+1;
        }
        if (root.left == null && root.right == null) {
            depth = 1 ;
        }
        if (root.left != null && root.right != null) {
            depth = Math.min(left,right)+1;
        }
        return depth;
    }
}

10、完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

1 2	输入：root = [1,2,3,4,5,6] 输出：6

示例 2：

1 2	输入：root = [] 输出：0

示例 3：

1 2	输入：root = [1] 输出：1

提示：

树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

class Solution {
    public int countNodes(TreeNode root) {
    int node = 0;
    if (root == null) {
        return 0 ;
    }
    int left = countNodes(root.left);
    int right = countNodes(root.right);
    node = left + right + 1;
    return node;
    }
}

class Solution {
    public int countNodes(TreeNode root) {
        int result = 0;
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()){
            int size = queue.size();
            while (size > 0) {
                TreeNode tmp = queue.poll();
                result++;
                size--;
                if (tmp.left != null) {
                    queue.offer(tmp.left);
                }
                if (tmp.right != null) {
                    queue.offer(tmp.right);
                } 
            }
        } 
        return result;
    }
}

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftdepth = 0;
        int rightdepth = 0;
        TreeNode tmp = root;
        while (tmp.right != null) {
            rightdepth++;
            tmp = tmp.right;
        }
        tmp = root;
        while (tmp.left != null) {
            leftdepth++;
            tmp = tmp.left;
        }
        if (leftdepth == rightdepth) {
            return (2<<rightdepth)-1;
        }
        return countNodes(root.left)+countNodes(root.right)+1;
    }
}

11、平衡二叉树

力扣题目链接

给定一个二叉树，判断它是否是

平衡二叉树

示例 1：

1 2	输入：root = [3,9,20,null,null,15,7] 输出：true

示例 2：

1 2	输入：root = [1,2,2,3,3,null,null,4,4] 输出：false

示例 3：

1 2	输入：root = [] 输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

 class Solution {
     public boolean isBalanced(TreeNode root) {
         if (root == null) {
             return true;
         }
         int left = subLength(root.left);
         int right = subLength(root.right);
         if (Math.abs(left-right) > 1) {
             return false;
         }
         return isBalanced(root.left) && isBalanced(root.right);

     }
     public int subLength(TreeNode root) {
         if (root == null) {
             return 0;
         }
         return Math.max(subLength(root.left),subLength(root.right))+1;
     }
}

class Solution {
    public boolean isBalanced(TreeNode root) {
        return getLength(root)==-1 ?false:true;

    }
    public int getLength(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // int result = 0;
        int leftLength = getLength(root.left);
        if (leftLength == -1) {
            return -1;
        }
        int rightLength = getLength(root.right);
        if (rightLength == -1) {
            return -1;
        }
        if (Math.abs(rightLength-leftLength) >1) {
            return -1;
        }
        return Math.max(rightLength,leftLength)+1;
    }
}

12、二叉树的所有路径

力扣题目链接

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

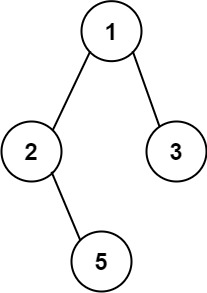
1 2	输入：root = [1,2,3,null,5] 输出：["1->2->5","1->3"]

示例 2：

1 2	输入：root = [1] 输出：["1"]

提示：

树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        List<Integer> paths = new ArrayList<>();
        Backtrace (root,res,paths);
        return res;

    }
    public void Backtrace(TreeNode root,List<String> res,List<Integer> paths) {
        paths.add(root.val);
        if (root.left == null && root.right == null) {
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i<paths.size()-1; i++) {
                sb.append(paths.get(i)).append("->");
            }
            sb.append(paths.get(paths.size()-1));
            res.add(sb.toString());
            return;
        }
        if (root.left != null) {
            Backtrace(root.left,res,paths);
            paths.remove(paths.size()-1);
        }
        if (root.right != null) {
            Backtrace(root.right,res,paths);
            paths.remove(paths.size()-1);
        }
    }
}

一直往下遍历，递归的终止条件时遇到左孩子和右孩子都为空，此时将路径转换为字符串并添加到结果列表，然后回溯到上一个节点继续遍历其他子节点。

13、左叶子之和

力扣题目链接

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

1
2
3

输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

1 2	输入: root = [1] 输出: 0

提示:

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

// 层序遍历迭代法
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        int sum = 0;
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size -- > 0) {
                TreeNode node = queue.poll();
                if (node.left != null) { // 左节点不为空
                    queue.offer(node.left);
                    if (node.left.left == null && node.left.right == null){ // 左叶子节点
                        sum += node.left.val;
                    }
                }
                if (node.right != null) queue.offer(node.right);
            }
        }
        return sum;
    }
}

使用层次遍历法，由于不能直接判断本节点是不是左叶子节点，所以需要借助父亲节点进行判断。

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        int leftVal = sumOfLeftLeaves(root.left);
        int rightVal = sumOfLeftLeaves(root.right);
        int midVal = 0;
        if (root.left != null && root.left.left==null && root.left.right==null) {
            midVal += root.left.val;
        }
        int result = leftVal + midVal +rightVal;
        return result;    
    }
}

14、找树左下角的值

力扣题目链接

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

1 2	输入: root = [2,1,3] 输出: 1

示例 2:

1 2	输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7

提示:

二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        int result = 0 ;
        Queue <TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()) {
            int length = queue.size();
            if (length > 0) {
                TreeNode tmp = queue.peek();
                result = tmp.val;
            }
            while (length > 0) {
                TreeNode tmp = queue.poll();
                if (tmp.left != null) {
                    queue.offer(tmp.left);
                }
                if (tmp.right != null) {
                    queue.offer(tmp.right);
                }
                length--;
            }
        }
        return result;
    }
}

class Solution {
    private int Deep = -1;
    private int value = 0;
    public int findBottomLeftValue(TreeNode root) {
        value = root.val;
        findLeftValue(root,0);
        return value;        
    }
    public void findLeftValue(TreeNode root,int deep) {
        if (root ==null) return;
        if (deep > Deep) {
            value = root.val;
            Deep = deep;
        }
        if (root.left !=null) {
            findLeftValue(root.left,deep+1);
        }
        if (root.right !=null) {
            findLeftValue(root.right,deep+1);
        }
    }
}

通过确定访问的变量是不是处于最大深度的节点来确定。

15、路径总和

力扣题目链接

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

1
2
3

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

1
2
3

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) return false;
        targetSum -= root.val;
        if (root.left == null && root.right == null) {
            return targetSum == 0;
        }
        if (root.left != null) {
            boolean leftResult = hasPathSum(root.left,targetSum);
            if (leftResult) {
                return true;
            }
        }
        if (root.right != null) {
            boolean rightResult = hasPathSum(root.right,targetSum);
            if (rightResult) {
                return true;
            }
        }
        return false;
    }
}

用目标结果减去节点的值判断是否为0 来确定是否存在具体的路径。

路径综合II

https://leetcode.cn/problems/path-sum-ii/

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

1 2	输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

1 2	输入：root = [1,2,3], targetSum = 5 输出：[]

示例 3：

1 2	输入：root = [1,2], targetSum = 0 输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> tmp = new ArrayList<>();
        pathFind(root,targetSum,tmp,result);
        return result;

    }
    public void pathFind(TreeNode root, int targetSum,List<Integer> tmp,List<List<Integer>> result) {
        if (root == null) return;
        tmp.add(root.val);
        targetSum -= root.val;
        if(root.left == null && root.right == null) {
            if (targetSum == 0) {
                // result.add(tmp);
                result.add(new ArrayList<>(tmp));
            } 
            return;
        }
        if(root.left != null) {
            pathFind(root.left,targetSum,tmp,result);
            tmp.remove(tmp.size()-1);

        }
        if(root.right != null) {
            pathFind(root.right,targetSum,tmp,result);
            tmp.remove(tmp.size()-1);
        }
    }
}

关键在于需要创建一个快照，因为直接使用引用的话，后续对tmp的修改会影响result中的数据。

16、从中序与后序遍历序列构建二叉树

力扣题目链接

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

1 2	输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出：[3,9,20,null,null,15,7]

示例 2:

1 2	输入：inorder = [-1], postorder = [-1] 输出：[-1]

class Solution {
    private Map<Integer,Integer>map;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        for (int i=0; i<inorder.length; i++) {
            map.put(inorder[i],i);
        }
        TreeNode result = buildTree (inorder,0,inorder.length-1,postorder,0,postorder.length-1);
        return result;
    }
    public TreeNode buildTree(int[] inorder, int inbegin, int inend, int[] postorder, int postbegin, int postend) {
        if (inbegin > inend || postbegin > postend) {
            return null;
        } 
        int rootVal = postorder[postend];
        int indexVal = map.get(rootVal);
        int leftSize = indexVal - inbegin;
        TreeNode root = new TreeNode(rootVal);
        root.left = buildTree (inorder,indexVal-leftSize,indexVal-1,postorder,postbegin,postbegin+leftSize-1);
        root.right = buildTree (inorder,indexVal+1,inend,postorder,postbegin+leftSize,postend-1);
        return root;
    }
}

https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

1 2	输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]

示例 2:

1 2	输入: preorder = [-1], inorder = [-1] 输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

class Solution {
    private Map <Integer,Integer> map;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        map = new HashMap<>();
        for (int i=0;i<inorder.length;i++) {
            map.put(inorder[i],i);
        }
        TreeNode result = buildTreeSolution(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
        return result;

    }
    public TreeNode buildTreeSolution (int[] preorder, int preBegin, int preEnd,int[] inorder, int inBegin, int inEnd) {
        if (preBegin > preEnd || inBegin > inEnd) {
            return null;
        }
        int rootVal = preorder[preBegin];
        int indexVal = map.get(rootVal);
        int leftSize = indexVal - inBegin;
        TreeNode root = new TreeNode(rootVal);
        root.left = buildTreeSolution(preorder,preBegin+1,preBegin+leftSize,inorder,inBegin,inBegin+leftSize);
        root.right = buildTreeSolution(preorder,preBegin+leftSize+1,preEnd,inorder,inBegin+leftSize+1,inEnd);
        return root;
    }
}

都是以前序或者后序的开头或最后的一个元素作为中序遍历数组的分界点。

17、最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 *最大二叉树* 。

示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

1 2	输入：nums = [3,2,1] 输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        if (nums.length == 0) {
            return null;
        }
        TreeNode result = construct(nums,0,nums.length-1);
        return result;
    }
    public TreeNode construct (int[] nums,int start, int end) {
        if (start > end) {
            return null;
        }
        int max = nums[start];
        int index = start ;
        for (int i = start; i <= end; i++) {
            if (nums[i] > max) {
                max = nums[i];
                index = i;
            }
        }
        TreeNode root = new TreeNode(max);
        root.left = construct(nums,start,index-1);
        root.right = construct(nums,index+1,end);
        return root;
    }
}

18、合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

1 2	输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出：[3,4,5,5,4,null,7]

示例 2：

1 2	输入：root1 = [1], root2 = [1,2] 输出：[2,2]

提示：

两棵树中的节点数目在范围 [0, 2000] 内
-104 <= Node.val <= 104

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null ) {
            return root2;
        }
        if (root2 == null) {
            return root1;
        }
        root1.val += root2.val;
        root1.left = mergeTrees(root1.left,root2.left);
        root1.right = mergeTrees(root1.right,root2.right);
        return root1;
    }

19、二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:

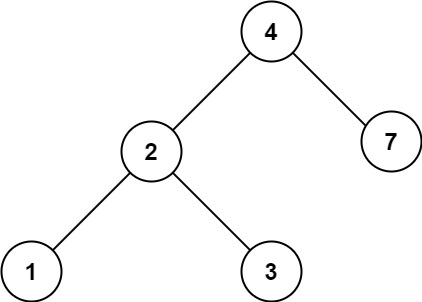
1 2	输入：root = [4,2,7,1,3], val = 2 输出：[2,1,3]

示例 2:

1 2	输入：root = [4,2,7,1,3], val = 5 输出：[]

提示：

树中节点数在 [1, 5000] 范围内
1 <= Node.val <= 107
root 是二叉搜索树
1 <= val <= 107

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        TreeNode left = searchBST(root.left, val);
        if (left != null) {
            return left;
        }
        return searchBST(root.right, val);
    }
}

20、验证二叉搜索树

力扣题目链接

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左

子树

只包含

小于

当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

1 2	输入：root = [2,1,3] 输出：true

示例 2：

1
2
3

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

class Solution {
    private long prev = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }    
        boolean left = isValidBST(root.left);
        if (!left) {
            return false;
        } 
        if (prev >= root.val) {
            return false;
        }
        prev = root.val;
        boolean right = isValidBST(root.right);
        return right;
    }
}

class Solution {
    public boolean isValidBST(TreeNode root) {
        List <Integer> list = new ArrayList<>();
        travel(root,list);
        for(int i = 1; i < list.size(); i++) {
            if (list.get(i) <= list.get(i-1)) {
                return false;
            }
        } 
        return true;    
    }
    public void travel(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        travel(root.left,list);
        list.add(root.val);
        travel(root.right,list);
    }

}

21、二叉搜索树的最小绝对差

力扣题目链接

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

1 2	输入：root = [4,2,6,1,3] 输出：1

示例 2：

1 2	输入：root = [1,0,48,null,null,12,49] 输出：1

提示：

树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105

class Solution {
    private Integer prev = null;
    private int min = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        travel(root);
        return min;
    }
    public void travel(TreeNode root) {
        if (root == null) {
            return;
        }
        travel(root.left);
        if (prev != null) {
            min = Math.min(min, root.val - prev);
        }
        prev = root.val;
        travel(root.right);
    }
}

22、二叉搜索树中的众数

力扣题目链接

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：

1 2	输入：root = [1,null,2,2] 输出：[2]

示例 2：

1 2	输入：root = [0] 输出：[0]

提示：

树中节点的数目在范围 [1, 104] 内
-105 <= Node.val <= 105

class Solution {
    private Integer prev = null;
    private int count = 0;
    private int maxCount = 0;
    private List<Integer> result = new ArrayList<>(); 

    public int[] findMode(TreeNode root) {
        travel(root);
        return result.stream().mapToInt(Integer::intValue).toArray();
        
    }
    public void travel (TreeNode root) {
        if (root == null) {
            return;
        }
        travel(root.left);
        if (prev == null || root.val != prev) {
            count = 1;
        } else {
            count++;
        }
        if (count == maxCount) {
            result.add(root.val);
        }
        if (count > maxCount ) {
            maxCount = count;
            result.clear();
            result.add(root.val);
        }
        prev = root.val;
        travel(root.right);
    }

23、二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

1
2
3

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

1
2
3

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

1 2	输入：root = [1,2], p = 1, q = 2 输出：1

提示：

树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) {
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if (left != null && right != null) {
            return root;
        }
        if (left != null) {
            return left;
        } else {
            return right;
        }                
    }
}

假设我们在一个节点 root 开始搜索 p 和 q：

**当前节点是否为 null**：如果当前节点是 null，那显然这个子树中没有 p 和 q，我们返回 null。
**当前节点是否是 p 或 q**：如果当前节点正好是 p 或 q，那么这个节点直接可能是公共祖先，我们返回这个节点。
递归查找左右子树：如果当前节点不是 p 或 q，我们继续在它的左子树和右子树中递归查找 p 和 q。
- 如果在左子树中找到一个非空结果，说明 p 或 q 在左子树中。
- 如果在右子树中找到一个非空结果，说明 p 或 q 在右子树中。
- 如果左右子树都返回非空的结果，说明 p 和 q 分别位于左右子树中，因此当前节点 root 就是它们的最近公共祖先。
- 如果只有一边返回了非空结果（例如左边有，右边没有），那说明 p 和 q 都位于左子树中，返回左边的结果。
返回值：递归的结果就是我们所要的最近公共祖先。

23、二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

1
2
3

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

1
2
3

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

// 迭代法
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while (root != null) {
            if (p.val < root.val && q.val < root.val) {
                root = root.left;
            }
            else if (p.val > root.val && q.val > root.val) {
                root = root.right;
            } else {
                return root;
            }
        }
        return null;       
    }
}

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }
        if (p.val < root.val && q.val < root.val) {
            TreeNode left = lowestCommonAncestor (root.left,p,q);
            if (left != null) {
                return left;
            }
        }
        if (p.val > root.val && q.val > root.val) {
            TreeNode right = lowestCommonAncestor(root.right ,p ,q);
            if (right != null) {
                return right;
            }
        }
        return root;
    }
}

24、二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回 任意有效的结果 。

示例 1：

1
2
3

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

1 2	输入：root = [40,20,60,10,30,50,70], val = 25 输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

1 2	输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出：[4,2,7,1,3,5]

提示：

树中的节点数将在 [0, 104]的范围内。
-108 <= Node.val <= 108
所有值 Node.val 是 独一无二 的。
-108 <= val <= 108
保证 val 在原始BST中不存在。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }
        if (root.val > val) {
            root.left = insertIntoBST(root.left,val);
        }
        if (root.val < val) {
            root.right = insertIntoBST(root.right,val);
        }
        return root;
    }
}

25、删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

1
2
3

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

1 2	输入: root = [], key = 0 输出: []

提示:

节点数的范围 [0, 104].
-105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
-105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return root;
        }
        if (root.val == key) {
            if (root.left == null) {
                return root.right;
            }
            if (root.right == null) {
                return root.left;
            }
            TreeNode cur = root.right;
            while(cur.left != null) {
                cur = cur.left;
            }
            cur.left = root.left;
            return root.right;
        } 
        if (root.val < key) {
            root.right = deleteNode (root.right,key);
        }
        if (root.val > key) {
            root.left = deleteNode (root.left,key);
        }
        return root;
    }
}

26、修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

1 2	输入：root = [1,0,2], low = 1, high = 2 输出：[1,null,2]

示例 2：

1 2	输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出：[3,2,null,1]

提示：

树中节点数在范围 [1, 104] 内
0 <= Node.val <= 104
树中每个节点的值都是唯一的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return root;
        }
        if (root.val < low) {
            return trimBST(root.right,low,high);
        }else if (root.val > high) {
            return trimBST(root.left,low,high);
        }else {
            root.left = trimBST(root.left,low,high);
            root.right = trimBST(root.right,low,high);
            return root;
        }
    }
}

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int val) { this.val = val; }
}

public class TrimBST {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        // 寻找新的根节点，使其在范围内
        while (root != null && (root.val < low || root.val > high)) {
            if (root.val < low) {
                root = root.right;
            } else if (root.val > high) {
                root = root.left;
            }
        }

        TreeNode current = root;
        // 修剪左子树
        while (current != null) {
            while (current.left != null && current.left.val < low) {
                current.left = current.left.right;
            }
            current = current.left;
        }

        current = root;
        // 修剪右子树
        while (current != null) {
            while (current.right != null && current.right.val > high) {
                current.right = current.right.left;
            }
            current = current.right;
        }

        return root;
    }

    public static void main(String[] args) {
        // 示例：构建二叉搜索树
        TreeNode root = new TreeNode(3);
        root.left = new TreeNode(0);
        root.right = new TreeNode(4);
        root.left.right = new TreeNode(2);
        root.left.right.left = new TreeNode(1);

        // 修剪范围
        int low = 1, high = 3;

        // 修剪二叉搜索树
        TrimBST trimmer = new TrimBST();
        TreeNode trimmedRoot = trimmer.trimBST(root, low, high);

        // 输出修剪后的树
        printTree(trimmedRoot);
    }

    // 辅助函数：按层打印二叉树
    private static void printTree(TreeNode root) {
        if (root == null) return;
        java.util.Queue<TreeNode> queue = new java.util.LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.print(node.val + " ");
            if (node.left != null) queue.offer(node.left);
            if (node.right != null) queue.offer(node.right);
        }
        System.out.println();
    }
}

27、将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵

平衡

二叉搜索树。

示例 1：

1
2
3

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

1
2
3

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedArrayToBST(nums, 0, nums.length-1);
    }
    public TreeNode sortedArrayToBST(int[] nums, int start, int end) {
        if(start > end) {
            return null;
        }
        int mid = start + (end - start)/2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = sortedArrayToBST(nums,start,mid-1);
        root.right = sortedArrayToBST(nums,mid+1,end);
        return root;    
    }
}

28、把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

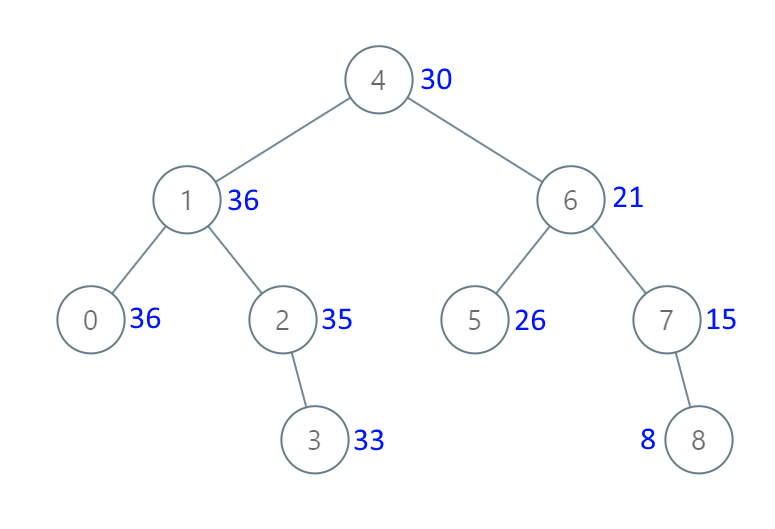
1 2	输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

1 2	输入：root = [0,null,1] 输出：[1,null,1]

示例 3：

1 2	输入：root = [1,0,2] 输出：[3,3,2]

示例 4：

1 2	输入：root = [3,2,4,1] 输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

class Solution {
    private int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        if (root == null) {
            return root;
        }
        convertBST(root.right);
        sum += root.val;
        root.val = sum;
        convertBST(root.left);
        return root;
    }
}

leetcode-二叉树

http://example.com/2024/01/29/leetcode-二叉树/

作者

John Doe

发布于

2024-01-29

更新于

2025-02-28

许可协议

#leetcode

You need to set install_url to use ShareThis. Please set it in _config.yml.

leetcode-二叉树

二叉树

1、二叉树的前序遍历

2、二叉树的后序遍历

3、二叉树的中序遍历

4、二叉树的统一迭代法

5、二叉树的层序遍历

7、对称二叉树

8、二叉树的最大深度

9、二叉树的最小深度

10、完全二叉树的节点个数

11、平衡二叉树

12、二叉树的所有路径

13、左叶子之和

14、找树左下角的值

15、路径总和

16、从中序与后序遍历序列构建二叉树

17、最大二叉树

18、合并二叉树

19、二叉搜索树中的搜索

20、验证二叉搜索树

21、二叉搜索树的最小绝对差

22、二叉搜索树中的众数

23、二叉树的最近公共祖先

23、二叉搜索树的最近公共祖先

24、二叉搜索树中的插入操作

25、删除二叉搜索树中的节点

26、修剪二叉搜索树

27、将有序数组转换为二叉搜索树

28、把二叉搜索树转换为累加树

作者

发布于

更新于

许可协议

喜欢这篇文章？打赏一下作者吧

评论

链接

分类

最新文章

归档

标签

订阅更新

follow.it